Secciķ a cārrec de Gottlob
|
FÍSICA APLICADA |
Secciķ a cārrec de Gottlob |
Petit càlcul: |
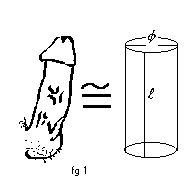
Nombre aproximat d’àtoms que conté el penis de Rocco Siffredi. |
Dades: |
Diàmetre: |
|
Longitud: |
||
Radi atòmic: |
r, un Armstrong |
El cālcul el realitzarem en base a una idea molt simple. Primer
calculem el volum del penis Vpenis, després el
volum que un àtom ocupa a l'espai Vātom. |
, que ens donarà el nombre de volums atòmics necessaris
per omplir el volum del penis; o el que es el mateix, com considerem que
al centre de cada volum atòmic hi ha un àtom, això
ens donarà directament el número aproximat d’àtoms
desitjat. |
 |
 b b |
filosòfics que comporta treballar sobre models fruit d'una abstracció més o menys ,(en aquest cas més), barroera de la natura.(Això ho dic per les més que probables crítiques que rebré del meu amic Iñigo). (... com tothom sap; la natura és una dama que no sol exhibir
de manera gratuïta tota la seva complexitat i bellesa. L'artista,
la sent i la descriu amb les potents i diàfanes armes de la sensibilitat
i l'esperit, la qual cosa dona fruit a l'admiració i complicitat
amb els seus congèneres (espectadors). El científic la sent
i la descriu amb les febles i fosques armes de l'anàlisi racional,
cosa que dona lloc a la creació dels models abans esmentats i a
una gran incomprensió i ànima aversió envers l’espectador.
Les diferències òbvies entre l'artista i el científic,
venen donades a l’hora de la descripció (comunicació),
però les més profundes, a les quals la gran majoria del
personal no té accés, sorgeixen a l’hora de sentir
la natura, i és en aquest primer estadi, al qual el científic
es porta la millor part del pastís. Per dir-ho d'una manera més
gràfica; l'artista li veu les tetes a la natura i ho explica als
altres, alguns científics, molt de tant en tant se la follen i
han de romandre en silenci. |
A qualsevol tractat de geometria bàsica es pot trobar que el volum d'un cilindre es igual a : |
, on |
es el diàmetre i |
la seva alçada. |
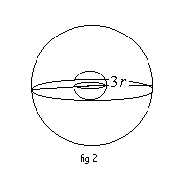
El volum d'una esfera de radi r es : |
Així doncs, substituint les dades numèriques obtenim: |
Hem posat 3 , perquè aquest es el radi de la nostra esfera. Si dividim aquestes dues magnituds obtenim: |
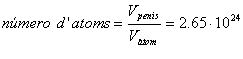 |
, que es el resultat desitjat. Per la gent familiaritzada amb una nomenclatura més química, podrà apreciar que aquest nombre correspon a 4.4 mols d'àtoms. |
( un mol = |
) |
Si hi ha alguna ànima curiosa, escriuré la fórmula que permet fer un càlcul personalitzat del nombre d'àtoms de cada individu, un cop coneguts la longitud i el diàmetre del seu "cacharro" |
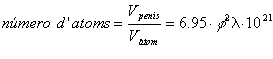 |
, si les mesures es donen en centímetres. |
Aquest humil redactor ha fet el càlcul, i ha vist que l’incommensurable Rocco, té aproximadament dos milers de milions de milions d'àtoms més que ell. Ja ho sabia jo, que no som ningú..... però.... ¿tant ningú? |